DDPM（概率扩散模型）直觉和背后的一些数学

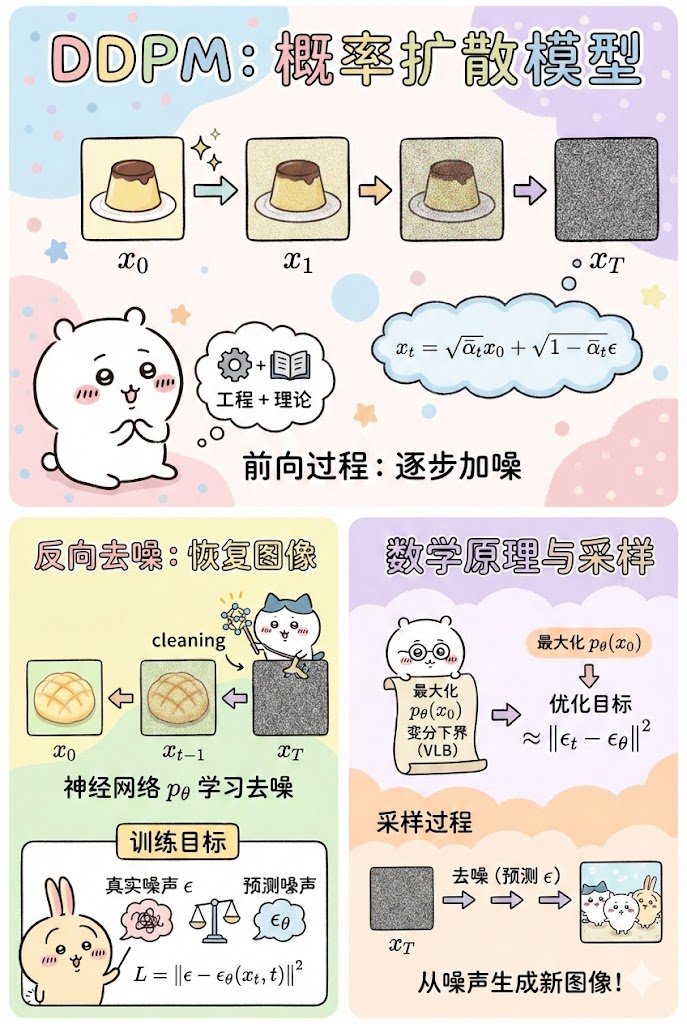
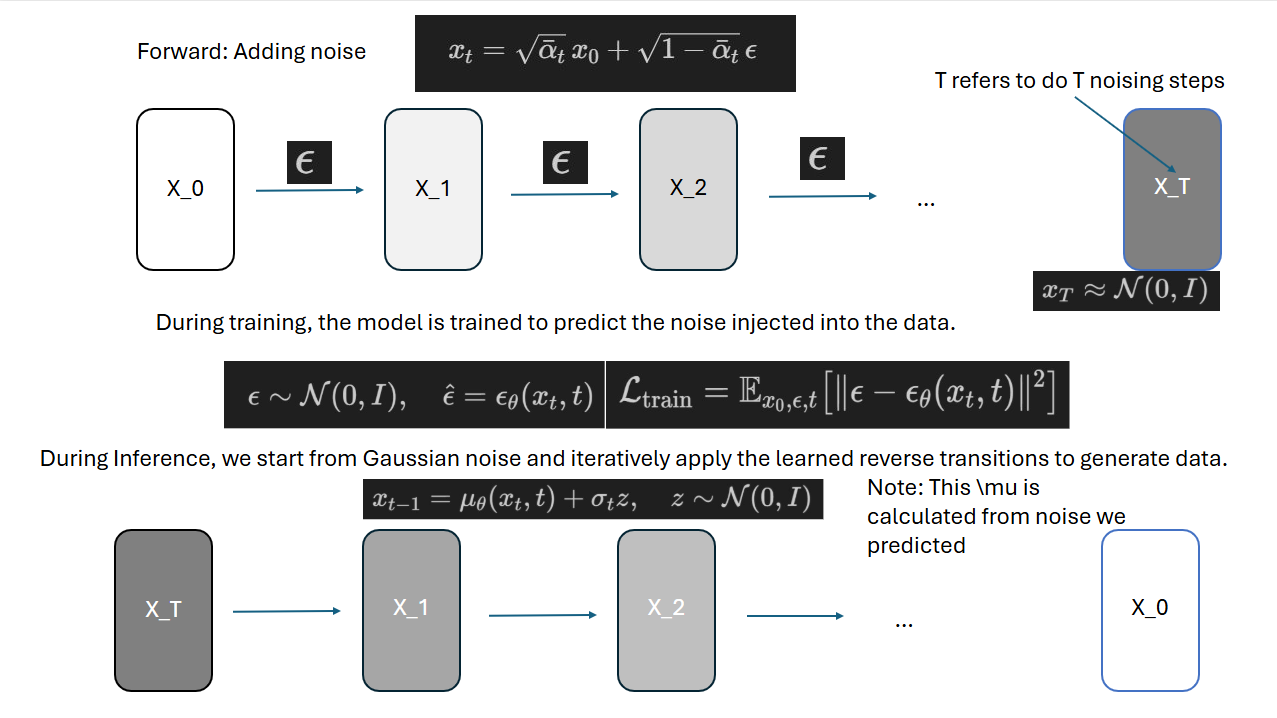
DDPM (Denoising Diffusion Probabilistic Models)

Introduction

Diffusion models 的成功并非源于某个直观的理论证明说明”这种方法一定更好”。事实上，它的优越性主要是通过实验发现的——研究者们尝试了这种方法，发现它在生成质量和多样性上表现出色。

有此可以得一窥泛AI本身就是一个工程和理论相互结合的一个领域,你在工程上能够反复迭代够快,你就可以test你的这些理论模型到底会不会work。你再去反过去用概率学来研究那些模型的原理,让它更加的make sense。

Diffusion models 受热力学启发，定义一个马尔可夫链逐步向数据添加噪声。

  • 前向过程 (Forward Process): 逐步向原始图像 添加高斯噪声，经过 步后得到纯噪声
  • 反向过程 (Reverse Process): 训练神经网络 学习去噪，从纯噪声 逐步恢复出原始图像

Forward process

给定

Adding noise ，at time , we add a noise sampled from gaussian to generate latents to ：

Single step transition：

重参数化技巧： 我们引入重参，它可以直接从 跳到任意时间步 ，无需逐步计算中间步骤。给定 和 ，我们有：

公式:

我们可以对他进行重参数化化简：

推导 (参考 Lilian Weng 的博客):

从单步转移公式开始，我们可以用重参数化改写：

现在递推，将 代入：

使用高斯合并，两个独立的高斯噪声 和 相加后仍是高斯分布 。

因此对于后面一项我们可以化简方差项：

其中 。

所以：

引入定义：，，则：

然后持续展开递推到 ：

Intuition:

  • : 保留原始信号的比例（随 递减）
  • : 添加噪声的比例（随 递增）
  • 通常 ，所以 ，噪声逐渐增强，不过这个可以自定义，很多实现都有自己的加噪scheduling算法。

Code

1. Beta Schedule 定义 (gaussian_diffusion.py:18-42)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def get_named_beta_schedule(schedule_name, num_diffusion_timesteps):
    """获取预定义的 beta 调度"""
    if schedule_name == "linear":
        # 原始 DDPM 的线性调度
        scale = 1000 / num_diffusion_timesteps
        beta_start = scale * 0.0001
        beta_end = scale * 0.02
        return np.linspace(beta_start, beta_end, num_diffusion_timesteps, dtype=np.float64)

    elif schedule_name == "cosine":
        # Improved DDPM 提出的余弦调度
        return betas_for_alpha_bar(
            num_diffusion_timesteps,
            lambda t: math.cos((t + 0.008) / 1.008 * math.pi / 2) ** 2,
        )

2. 系数预计算 (gaussian_diffusion.py:140-151)

1
2
3
4
5
6
7
8
# 在 GaussianDiffusion.__init__ 中
alphas = 1.0 - betas                              # α_t = 1 - β_t
self.alphas_cumprod = np.cumprod(alphas, axis=0)  # ᾱ_t = ∏α_s
self.alphas_cumprod_prev = np.append(1.0, self.alphas_cumprod[:-1])  # ᾱ_{t-1}

# 前向扩散 q(x_t | x_0) 的系数
self.sqrt_alphas_cumprod = np.sqrt(self.alphas_cumprod)           # √ᾱ_t
self.sqrt_one_minus_alphas_cumprod = np.sqrt(1.0 - self.alphas_cumprod)  # √(1-ᾱ_t)

3. 前向加噪 q_sample (gaussian_diffusion.py:188-206)

1
2
3
4
5
6
7
8
9
10
11
12
def q_sample(self, x_start, t, noise=None):
    """
    前向扩散：从 q(x_t | x_0) 采样
    实现公式: x_t = √ᾱ_t · x_0 + √(1-ᾱ_t) · ε
    """
    if noise is None:
        noise = th.randn_like(x_start)

    return (
        _extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
        + _extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise
    )

4. 辅助函数：提取系数 (gaussian_diffusion.py:828-841)

1
2
3
4
5
6
7
8
9
def _extract_into_tensor(arr, timesteps, broadcast_shape):
    """
    从 1-D 数组中根据 timesteps 索引提取值，并广播到目标形状
    例如：arr=[a0,a1,...,aT], timesteps=[3,5,2] → 提取 [a3,a5,a2] 并扩展维度
    """
    res = th.from_numpy(arr).to(device=timesteps.device)[timesteps].float()
    while len(res.shape) < len(broadcast_shape):
        res = res[..., None]  # 增加维度以便广播
    return res.expand(broadcast_shape)

公式对应:

论文符号 代码变量
alphas_cumprod[t]
sqrt_alphas_cumprod[t]
sqrt_one_minus_alphas_cumprod[t]
x_start
noise
返回值

反向去噪

Intuition

数学原理表明，当 足够小时，每一步加噪声的逆操作也满足正态分布：

这是一个关键的理论基础——它告诉我们反向过程的函数形式是已知的（高斯分布），我们只需要学习它的参数（均值 和方差 ）。

如果我们知道精确的反向分布 ，就可以：

  1. 从纯噪声采样
  2. 逐步反向运行，得到 的样本

现在我们来用神经网络 来近似（均值 和方差 ）。）

公式 (3): 神经网络建模反向过程

符号解释:

符号 含义
由参数 的神经网络建模的分布
要生成的更清晰图像
当前噪声图像（条件）
网络预测的均值（去噪后的期望值）
网络预测的协方差（不确定性）

训练好之后怎么采样：

我们可以把diffusion的前项abstract成一个编码器，和后向abstract成一个解码器。

  • - 将图像编码成噪声
  • - 从噪声解码回图像

就会发现diffusion就是一个大号的VAE。

后验分布的贝叶斯推导

直觉上我们需要让真实的后验分布（）和我们预测的分布 对齐（也就是让他们之间的散度变小），我们来简化后验分布（的公式。

直接计算 需要整个数据分布，但如果我们知道 ，就可以用贝叶斯定理：

由于马尔可夫性质，，我们已知：

反向过程的真实后验

当我们知道 和 时，可以用贝叶斯定理计算反向一步的精确分布，我们得到后验方差和后验均值，此处省略推到，具体看附录。

均值的重参数化：预测噪声

问题: 后验均值 依赖 ，但推理时我们没有 。

解决方案: 从前向过程的重参数化公式出发，反推 ：

解出 ：

将这个代入后验均值 ：

化简后得到均值的噪声形式：

Intuition:

  • 神经网络只需预测噪声
  • 均值
  • 这样就不需要显式预测 了

训练目标：预测噪声

神经网络学习预测添加的噪声 ，训练损失为：

其中：

  • 是前向过程采样的真实噪声
  • 是网络预测的噪声

训练流程:

  1. 从训练集采样
  2. 随机采样时间步
  3. 采样噪声
  4. 计算
  5. 网络预测
  6. 计算损失 ，反向传播

推理流程:

  1. 从纯噪声开始
  2. 对 ：
    • 预测噪声：
    • 计算均值：
    • 采样：，其中 （ 时 ）
  3. 返回

对应代码

预测噪声并恢复 x_0 gaussian_diffusion.py:328-349:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def _predict_xstart_from_eps(self, x_t, t, eps):
    # 从噪声预测 x_0: x_0 = (x_t - √(1-ᾱ_t)·ε) / √ᾱ_t
    assert x_t.shape == eps.shape
    return (
        _extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
        - _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * eps
    )

def _predict_eps_from_xstart(self, x_t, t, pred_xstart):
    # 反向：从 x_0 预测噪声 ε = (x_t - √ᾱ_t·x_0) / √(1-ᾱ_t)
    return (
        _extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
        - pred_xstart
    ) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape)

其中预计算了 gaussian_diffusion.py:150-151:

1
2
3
4
5
self.sqrt_recip_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod)
# 1/√ᾱ_t

self.sqrt_recipm1_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod - 1)
# √(1/ᾱ_t - 1) = √((1-ᾱ_t)/ᾱ_t)

训练损失 gaussian_diffusion.py:677-750:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def training_losses(self, model, x_start, t, model_kwargs=None, noise=None):
    if model_kwargs is None:
        model_kwargs = {}
    if noise is None:
        noise = th.randn_like(x_start)

    # 前向加噪：x_t = √ᾱ_t·x_0 + √(1-ᾱ_t)·ε
    x_t = self.q_sample(x_start, t, noise=noise)

    # 神经网络预测
    model_output = model(x_t, self._scale_timesteps(t), **model_kwargs)

    # 根据 model_mean_type 确定目标
    target = {
        ModelMeanType.PREVIOUS_X: self.q_posterior_mean_variance(
            x_start=x_start, x_t=x_t, t=t
        )[0],
        ModelMeanType.START_X: x_start,      # 直接预测 x_0
        ModelMeanType.EPSILON: noise,         # 目标是真实噪声
    }[self.model_mean_type]

    terms["mse"] = mean_flat((target - model_output) ** 2)
    # ...

采样过程 gaussian_diffusion.py:356-387:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def p_sample(self, model, x, t, clip_denoised=True, denoised_fn=None, model_kwargs=None):
    # 获取均值和方差
    out = self.p_mean_variance(
        model, x, t,
        clip_denoised=clip_denoised,
        denoised_fn=denoised_fn,
        model_kwargs=model_kwargs,
    )
    noise = th.randn_like(x)
    nonzero_mask = (
        (t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
    )  # t=0 时不加噪声

    # 采样：x_{t-1} = μ_θ + σ·z
    sample = out["mean"] + nonzero_mask * th.exp(0.5 * out["log_variance"]) * noise
    return {"sample": sample, "pred_xstart": out["pred_xstart"]}

系数预计算 gaussian_diffusion.py:153-169:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 公式 (10): β̃_t = β_t * (1 - ᾱ_{t-1}) / (1 - ᾱ_t)
self.posterior_variance = (
    betas * (1.0 - self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)

# log calculation clipped because the posterior variance is 0 at the beginning
self.posterior_log_variance_clipped = np.log(
    np.append(self.posterior_variance[1], self.posterior_variance[1:])
)

# 公式 (11) 的两个系数:
# x_0 的系数: √ᾱ_{t-1} * β_t / (1 - ᾱ_t)
self.posterior_mean_coef1 = (
    betas * np.sqrt(self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)

# x_t 的系数: √α_t * (1 - ᾱ_{t-1}) / (1 - ᾱ_t)
self.posterior_mean_coef2 = (
    (1.0 - self.alphas_cumprod_prev) * np.sqrt(alphas) / (1.0 - self.alphas_cumprod)
)

计算后验分布 gaussian_diffusion.py:208-230:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def q_posterior_mean_variance(self, x_start, x_t, t):
    """
    Compute the mean and variance of the diffusion posterior:
        q(x_{t-1} | x_t, x_0)
    """
    # 公式 (11): μ̃_t(x_t, x_0)
    posterior_mean = (
        _extract_into_tensor(self.posterior_mean_coef1, t, x_t.shape) * x_start  # 第一项
        + _extract_into_tensor(self.posterior_mean_coef2, t, x_t.shape) * x_t    # 第二项
    )
    posterior_variance = _extract_into_tensor(self.posterior_variance, t, x_t.shape)  # 公式 (10)
    posterior_log_variance_clipped = _extract_into_tensor(
        self.posterior_log_variance_clipped, t, x_t.shape
    )
    return posterior_mean, posterior_variance, posterior_log_variance_clipped

使用后验分布 gaussian_diffusion.py:232-326:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def p_mean_variance(self, model, x, t, clip_denoised=True, denoised_fn=None, model_kwargs=None):
    # 神经网络预测
    model_output = model(x, self._scale_timesteps(t), **model_kwargs)

    # 根据 model_mean_type 获取 pred_xstart
    if self.model_mean_type == ModelMeanType.START_X:
        pred_xstart = process_xstart(model_output)
    else:  # ModelMeanType.EPSILON
        pred_xstart = process_xstart(
            self._predict_xstart_from_eps(x_t=x, t=t, eps=model_output)
        )

    if clip_denoised:
        pred_xstart = pred_xstart.clamp(-1, 1)

    # 用预测的 x_0 计算后验分布 (公式 12)
    model_mean, _, _ = self.q_posterior_mean_variance(
        x_start=pred_xstart, x_t=x, t=t
    )
    return {
        "mean": model_mean,
        "variance": model_variance,
        "log_variance": model_log_variance,
        "pred_xstart": pred_xstart,
    }

公式对应表

论文符号 代码变量 含义
alphas_cumprod[t] 累积信号保留率
alphas_cumprod_prev[t] 前一步的累积信号保留率
betas[t] 前向噪声调度
alphas[t]
sqrt_alphas_cumprod[t] 信号系数
sqrt_one_minus_alphas_cumprod[t] 噪声系数
sqrt_recip_alphas_cumprod[t] 恢复 的系数
sqrt_recipm1_alphas_cumprod[t] 噪声恢复系数
posterior_variance[t] 后验方差 (公式 10)
posterior_mean 后验均值 (公式 11)
$q(x_{t-1} \ x_t, x_0)$ q_posterior_mean_variance() 后验分布 (公式 12)
model_output (when model_mean_type=EPSILON) 网络预测的噪声
的预测 pred_xstart 从噪声恢复的

优化目标

以上介绍了前向过程、反向过程以及训练时预测噪声的损失函数，直觉上我们能够基本确定让噪声接近对方几乎就是对的，但我们还没有数学上的解释。

扩散概率模型名字之所以有”概率”二字，是因为这个模型是在描述一个系统的概率。准确来说，扩散模型是在描述反向过程生成出某一项数据的概率。也就是说，扩散模型 是一个有着可训练参数 的模型，它描述了反向过程生成出数据 的概率。 满足 ，其中 就是我们熟悉的反向过程，只不过它是以概率计算的形式表达：

上一节里见到的优化目标，是让去噪声操作 和加噪声操作的逆操作 尽可能相似。然而，这个描述并不确切。扩散模型原本的目标，是最大化 这个概率，其中 是来自训练集的数据。换个角度说，给定一个训练集的数据 ，经过前向过程和反向过程，扩散模型要让复原出 的概率尽可能大。这也是我们在本文开头认识 VAE 时见到的优化目标。

变分下界（VLB）

最大化 ，一般会写成最小化其负对数值，即最小化 。使用和 VAE 类似的变分推理，可以把优化目标转换成优化一个叫做变分下界（variational lower bound, VLB）的量。它最终可以写成：

这里的 表示分布 P 和 Q 之间的 KL 散度。如果 , 都是正态分布，则它们的 KL 散度可以由一个简单的公式给出。

其中，第一项 和可学习参数 无关（因为可学习参数只描述了每一步去噪声操作，也就是只描述了 ），可以不去管它。那么这个优化目标就由两部分组成：

  1. 最小化 ：表示的是最大化每一个去噪声操作和加噪声逆操作的相似度
  2. 最小化 ：就是已知 时，让最后复原原图 概率更高

KL 散度项的简化

我们来看第一部分是怎么计算的。首先回顾一下正态分布之间的 KL 散度公式。设一维正态分布 , 的公式如下：

则：

而对于 ，根据前文的分析，我们知道，待求方差 可以直接由计算得到：

两个正态分布方差的比值是常量。所以，在计算 KL 散度时，不用管方差那一项了，只需要均值那一项：

由根据之前的均值公式：

这一部分的优化目标可以化简成：

DDPM 论文指出，如果把前面的系数全部丢掉的话，模型的效果更好。最终，我们就能得一个非常简单的优化目标：

这就是我们上一节见到的优化目标。

重构项

还优化目标里还有 这一项。它的形式为：

只管后面有 的那一项（注意，）：

由于 ，代入后化简：

这和那些 KL 散度项 时的形式相同，我们可以用相同的方式简化优化目标，只保留 。这样，损失函数的形式全都是 了。

附录：后验分布 的数学推导

目标：从贝叶斯公式出发，推导出后验均值 和后验方差 。

Step 1: 贝叶斯公式

三个已知的高斯分布：

Step 2: 写出概率密度的指数部分

高斯分布 的概率密度正比于 。

后验分布的指数部分为（忽略归一化常数）：

Step 3: 展开并整理成关于 的二次型

展开括号内的表达式，只保留与 相关的项：

整理成标准形式 ：

由于 ，分子化简：

所以：

Step 4: 得到后验方差

对于高斯分布， 的系数给出方差：

Step 5: 得到后验均值

高斯分布的均值 ：

代入 ：

最终结果

其中：

  • 后验方差：
  • 后验均值：

reference

  1. https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
  2. https://zhuanlan.zhihu.com/p/638442430
  3. https://www.zhihu.com/question/658056360