VAE(变分自编码器)

1. INTRO

preq:

• 交叉熵、KL 散度、MSE、autoencoder

代码对应主要参考 models/vanilla_vae.py。

Intuition：希望构建一个从隐变量$Z$生成目标数据$X$的模型。同时我们希望这个$Z$是来自一个常见的分布，比如说正态。

目的都是进行分布之间的变换。

2. 从 Autoencoder的不足开始

• 经典 Autoencoder：编码器将输入 $x$ 映射到低维表示 $z$，解码器再重建 $\tilde x$。最常见目标是重建误差，例如均方误差 $\ell_{\text{rec}} = \lVert x - \tilde x \rVert_2^2$。

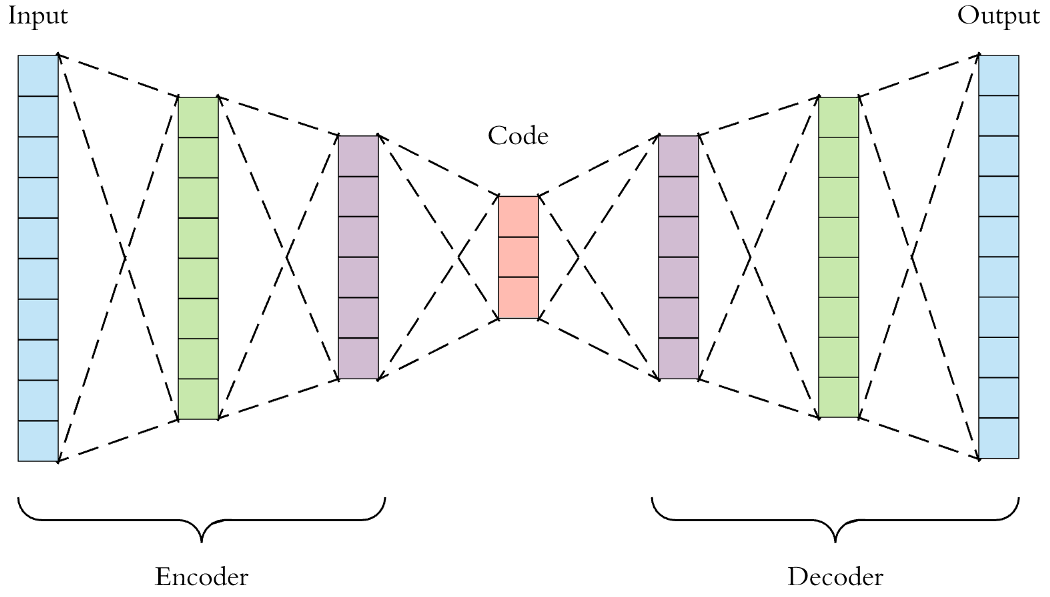
• 生成能力不足：训练好的解码器确实能将“合理的”潜变量解码成数据，但我们并不知道“合理的 $z$”在潜空间中的分布，因为随机构造 $z$ 往往落在训练分布之外，生成的只是噪声。

若能显式约束潜变量Z服从一个可采样的先验（常用 $p(z)=\mathcal N(0, I)$），再训练解码器学到 $p(x\mid z)$，那么从先验采样的 $z$ 也能生成有意义的样本，这就是VAE的思路。

Autoencoder小总

• 符号：数据集 ${x_i}_{i=1}^N$，编码器 $g_\phi: \mathbb R^{C\times H\times W} \to \mathbb R^d$，解码器 $f_\theta: \mathbb R^d \to \mathbb R^{C\times H\times W}$。
• 前向：$z = g_\phi(x)$，$\tilde x = f_\theta(z)$。
• Loss（MSE） $$\mathcal L_{\text{MSE}}(\theta, \phi) = \frac{1}{N}\sum_{i=1}^N \lVert x_i - f_\theta(g_\phi(x_i)) \rVert_2^2$$
• 为何生成失败：训练期间 $z$ 的支持集局限在编码器产出的“流形”上，未对 $p(z)$ 做约束。随机采样 $z \sim \text{Uniform or } \mathcal N(0,I)$ 往往落在流形外，使 $f_\theta(z)$ 解码出噪声。

3. VAE 初现：为何引入后验分布

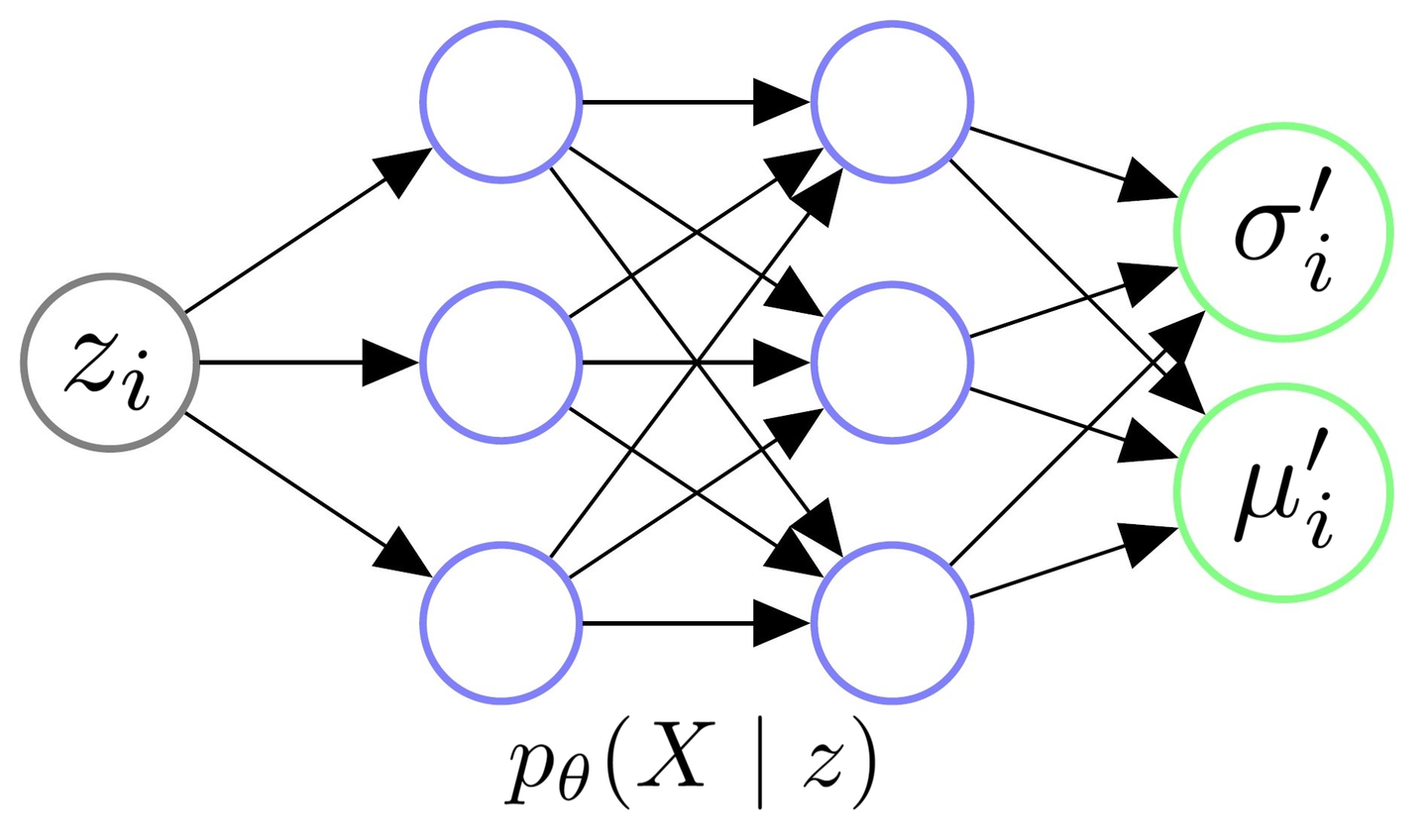
3.1 仅有 Decoder为什么不行

假设有一个简单想法：只用 decoder $p_\theta(x\mid z)$ 来生成，先验为 $p(z) = \mathcal N(0, I)$。

• 生成模型设定：

  • 先验：$p(z) = \mathcal N(0, I)$
  • 似然：$p_\theta(x \mid z) = \mathcal N(x; \mu_\theta(z), \sigma_\theta^2(z) \cdot I)$
  • 边际似然：$p_\theta(x) = \int p_\theta(x\mid z) p(z) \, dz$

• 为什么不行：

  • 计算困难：边际似然涉及对所有可能的 $z$ 积分，对于高维问题这是计算不可行的。
  • 参数估计困难：要用 MLE（最大似然估计）或 MAP（最大后验估计）来训练 $\theta$，需要计算或近似 $\log p_\theta(x)$，但它依赖这个积分，通常无法直接优化。
  • 采样困难：即使知道了 $p_\theta(x)$，要从中采样一个数据点 $x$ 也很困难——你不能直接从 $p_\theta(x)$ 采样，通常需要先从 $p(z)$ 采样再通过 decoder，但这受限于 decoder 的有限表达能力。

3.2 为什么需要变分后验近似

关键问题：我们怎样计算真实的后验 $p_\theta(z\mid x_i)$ ？

根据贝叶斯法则：

$$p_\theta(z \mid x_i) = \frac{p_\theta(x_i \mid z) p(z)}{p_\theta(x_i)} = \frac{p_\theta(x_i \mid z) p(z)}{\int_z p_\theta(x_i \mid z) p(z) \, dz}$$

为什么困难：

• 分母涉及对所有可能 $z$ 的积分，在高维空间中计算不可行。
• 即使知道了解码器 $p_\theta(x\mid z)$ 和先验 $p(z)$，我们也无法直接计算后验 $p_\theta(z\mid x)$。
• 在高维情况下，后验 $p_\theta(z\mid x)$ 本身也是一个高维分布，精确推断（exact inference）基本不可能。

解决方案：用一个可学习的分布 $q_\phi(z\mid x)$ 来近似真实后验。如果 $q_\phi(z\mid x)$ 足够好地拟合 $p_\theta(z\mid x)$，我们就能通过编码器得到每个 $x_i$ 对应的 $z$ 的分布！

3.3 用神经网络参数化后验分布

怎么用神经网络拟合一个后验分布？方法很简单：

1. 假设后验的函数形式：我们不需要完全刻画，只需指定它服从哪种分布（例如高斯）。
2. 用网络参数化分布参数：对于高斯分布，我们只需要学出均值和方差。
3. 编码器输出这些参数。

在 VAE 中，我们假设：

$$q_\phi(z\mid x) = \mathcal N\big(z; \mu_\phi(x), \sigma_\phi^2(x) \cdot I\big)$$

其中：

• $\mu_\phi(x), \log\sigma_\phi^2(x)$ 由编码器网络输出（参数为 $\phi$）
• 对角协方差结构使得 $z$ 的各维度相互独立，简化了计算

直观理解：编码器不再输出确定的 $z$，而是输出一个分布的参数。这样对每个输入 $x$，我们得到一个”专属”的后验分布 $q_\phi(z\mid x)$。

• 代码对应（models/vanilla_vae.py）：

  def encode(self, input: Tensor) -> List[Tensor]:
      result = self.encoder(input)
      result = torch.flatten(result, start_dim=1)
      mu = self.fc_mu(result)
      log_var = self.fc_var(result)
      return [mu, log_var]

  返回 $\mu_\phi(x)$ 和 $\log\sigma_\phi^2(x)$，完全确定了分布 $q_\phi(z\mid x)$。

3.4 重参数化技巧（Reparameterization Trick）

为了让梯度能反向传播到编码器，我们使用重参数化技巧：

• 公式：

  $$z = \mu + \sigma \odot \epsilon, \quad \epsilon \sim \mathcal N(0, I)$$

  其中 $\sigma = \sqrt{\exp(\log\sigma^2)}$，$\odot$ 表示元素级乘积。

• 为什么需要：如果直接从 $\mathcal N(\mu, \sigma^2)$ 采样，采样操作本身不可微，梯度无法穿过。重参数化把采样过程分离为：固定的噪声 $\epsilon$（可微信号通过）+ 确定的线性变换（参数 $\mu, \sigma$ 完全可微）。

• 代码对应（models/vanilla_vae.py）：

  def reparameterize(self, mu: Tensor, logvar: Tensor) -> Tensor:
      std = torch.exp(0.5 * logvar)
      eps = torch.randn_like(std)
      return eps * std + mu

  这正是 $z = \mu + \sigma \odot \epsilon$ 的实现。

3.5 完整架构总结

VAE 包含三个核心部分，如下图所示：

1. 编码器 $q_\phi(z\mid x)$：

• 输入：数据 $x$
• 输出：后验分布的参数 $\mu_\phi(x), \log\sigma_\phi^2(x)$
• 本质：参数化了 $p_\theta(z\mid x)$ 的变分近似

2. 采样层（重参数化）：

• 从分布 $q_\phi(z\mid x)$ 采出一个样本 $z$
• 保证梯度可通过

3. 解码器 $p_\theta(x\mid z)$：

• 输入：隐变量 $z$
• 输出：重建分布的参数 $\mu_\theta(z), \log\sigma_\theta^2(z)$
• 本质：学习从 $z$ 生成 $x$ 的条件分布

完整前向流程：

def forward(self, input: Tensor, **kwargs) -> List[Tensor]:
    mu, log_var = self.encode(input)           # 编码器输出后验参数
    z = self.reparameterize(mu, log_var)      # 采样 z
    return [self.decode(z), input, mu, log_var]  # 解码 + 返回参数供loss计算

至此，我们有了一个由两个网络（编码器、解码器）组成的完整的 VAE 结构，两者都是参数化的概率分布。下一步需要定义合理的训练目标，即 ELBO 损失函数。

4. ELBO 与损失函数推导

4.1 Evidence Lower Bound (ELBO)

我们的目标是最大化数据的对数似然 $\log p_\theta(x)$。利用已知的变分后验 $q_\phi(z\mid x)$

推导：

$$\log p_\theta(x) = \int q_\phi(z\mid x) \log p_\theta(x) \, dz \quad \text{（$q$中的全概率公式）}$$

利用贝叶斯法则 $p_\theta(x,z) = p_\theta(x\mid z) p(z)$：

$$\log p_\theta(x) = \int q_\phi(z\mid x) \log \frac{p_\theta(x,z)}{p_\theta(z\mid x)} \, dz$$

分子分母同时乘以 $q_\phi(z\mid x)$：

$$\log p_\theta(x) = \int q_\phi(z\mid x) \log \frac{p_\theta(x,z)}{q_\phi(z\mid x)} \, dz + \int q_\phi(z\mid x) \log \frac{q_\phi(z\mid x)}{p_\theta(z\mid x)} \, dz$$

第一项是 ELBO，第二项是 KL 散度：

$$\log p_\theta(x) = \underbrace{\int q_\phi(z\mid x) \log \frac{p_\theta(x,z)}{q_\phi(z\mid x)} \, dz}_{\text{ELBO}} + \underbrace{\operatorname{KL}\big(q_\phi(z\mid x) \| p_\theta(z\mid x)\big)}_{\text{KL} \ge 0}$$

因为 $\operatorname{KL} \ge 0$，所以：

$$\log p_\theta(x) \ge \mathcal L(p_\theta, q_\phi) := \int q_\phi(z\mid x) \log \frac{p_\theta(x,z)}{q_\phi(z\mid x)} \, dz$$

这就是 Evidence Lower Bound (ELBO)。

直观理解：

• 我们无法直接优化 $\log p_\theta(x)$（分母涉及积分）
• 但可以优化它的下界 ELBO，下界越紧，说明 $q_\phi(z\mid x)$ 越接近真实后验 $p_\theta(z\mid x)$
• 最大化 ELBO 等价于两个目标：拟合数据（重建）+ 让变分后验接近先验（正则化）

4.2 ELBO 的进一步展开

将 ELBO 改写成更容易计算的形式：

$$\mathcal L(p_\theta, q_\phi) = \int q_\phi(z\mid x) \log \frac{p_\theta(x,z)}{q_\phi(z\mid x)} \, dz$$ $$= \int q_\phi(z\mid x) \log \frac{p_\theta(x\mid z) p(z)}{q_\phi(z\mid x)} \, dz$$ $$= \int q_\phi(z\mid x) \log p_\theta(x\mid z) \, dz + \int q_\phi(z\mid x) \log \frac{p(z)}{q_\phi(z\mid x)} \, dz$$ $$= \mathbb E_{q_\phi}[\log p_\theta(x\mid z)] - \operatorname{KL}\big(q_\phi(z\mid x) \| p(z)\big)$$

两项含义：

• 第一项 $\mathbb E_{q_\phi}[\log p_\theta(x\mid z)]$：重建项，希望解码器能从采样的 $z$ 重建出 $x$
• 第二项 $-\operatorname{KL}(q_\phi | p)$：正则项，惩罚变分后验远离先验

4.3 KL 散度的闭式解

对于高斯分布，KL 散度有闭式解。

设 $q_\phi(z\mid x) = \mathcal N(\mu, \sigma^2 I)$，$p(z) = \mathcal N(0, I)$，则：

$$\operatorname{KL}\big(\mathcal N(\mu, \sigma^2) \| \mathcal N(0, 1)\big) = \frac{1}{2} \sum_{j=1}^d \big(-1 + \sigma_j^2 + \mu_j^2 - \log \sigma_j^2\big)$$

或等价地写成（用 $\sigma^2 = \exp(\log\sigma^2)$）：

$$\operatorname{KL} = -\frac{1}{2} \sum_{j=1}^d \big(1 + \log \sigma_j^2 - \mu_j^2 - \sigma_j^2\big)$$

KL Loss推导：

• 从定义出发：$\operatorname{KL}(q|p)=\int q(z) \log \frac{q(z)}{p(z)} dz$。
• 代入 $q(z)=\mathcal N(\mu, \sigma^2)$，$p(z)=\mathcal N(0,1)$，化简得到 $$\operatorname{KL}(q\|p) = -\tfrac12 (1 + \log \sigma^2 - \mu^2 - \sigma^2)$$
• 多维对角协方差时各维独立，求和即得上式。

代码对应（models/vanilla_vae.py 中 loss_function()）：

kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim=1), dim=0)

这正是上式的实现，其中 log_var = log σ²。

4.4 重建项的近似

对于重建项 $\mathbb E_{q_\phi}[\log p_\theta(x\mid z)]$，我们通常假设解码器输出的分布。

假设：解码器 $p_\theta(x\mid z)$ 为各像素独立的高斯：

$$p_\theta(x\mid z) = \mathcal N\big(x; \mu_\theta(z), \sigma^2 I\big)$$

其中方差 $\sigma^2$ 是一个固定的常数或学习的参数。

在这个假设下：

$$\log p_\theta(x\mid z) = -\frac{1}{2\sigma^2} \lVert x - \mu_\theta(z) \rVert_2^2 + \text{const}$$

因此：

$$\mathbb E_{q_\phi}[\log p_\theta(x\mid z)] \approx -\frac{1}{2\sigma^2} \mathbb E_{q_\phi}[\lVert x - \mu_\theta(z) \rVert_2^2]$$

忽略常数，这等价于最小化 MSE 重建误差。

代码对应（models/vanilla_vae.py）：

recons_loss = F.mse_loss(recons, input)

这里 recons 是解码器的输出（重建的 $x$），input 是原始输入。

4.5 完整损失函数

结合重建项和 KL 项，VAE 的完整损失函数为：

$$\mathcal L(\theta, \phi) = -\frac{1}{n}\sum_{i=1}^n \mathbb E_{q_\phi}[\log p_\theta(x_i\mid z_i)] + \frac{1}{n}\sum_{i=1}^n \operatorname{KL}\big(q_\phi(z\mid x_i) \| p(z)\big)$$

最终forward

对于一个样本 $x$，编码器给出 $\mu, \log\sigma^2$。采样 $z = \mu + \sigma \odot \epsilon$，其中 $\epsilon \sim \mathcal N(0, I)$。

重建项：

$$L_{\text{recon}} = \lVert x - \text{decode}(z) \rVert_2^2$$

KL 项：

$$L_{\text{KL}} = -\frac{1}{2} \sum_j (1 + \log\sigma_j^2 - \mu_j^2 - \sigma_j^2)$$

总损失：

$$L = L_{\text{recon}} + \beta \cdot L_{\text{KL}}$$

其中 $\beta$ 是一个权重参数（代码中为 kld_weight = M_N，用于批大小缩放）。

代码对应（models/vanilla_vae.py）：

def loss_function(self, *args, **kwargs) -> dict:
    recons = args[0]
    input = args[1]
    mu = args[2]
    log_var = args[3]
    
    kld_weight = kwargs['M_N']  # 批大小权重
    recons_loss = F.mse_loss(recons, input)
    
    kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim=1), dim=0)
    
    loss = recons_loss + kld_weight * kld_loss
    return {'loss': loss, 'Reconstruction_Loss': recons_loss.detach(), 'KLD': -kld_loss.detach()}

reference

1. https://zhuanlan.zhihu.com/p/348498294
2. https://arxiv.org/pdf/1906.02691
3. 代码：https://github.com/AntixK/PyTorch-VAE/blob/master/models/vanilla_vae.py
4. https://spaces.ac.cn/archives/5253